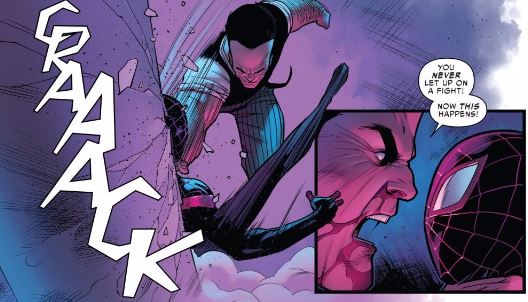Hey – want some advice for how to fight Hammerhead, Spider-Man?
Don’t.
You want more? Sure – three words: blunt force trauma.
Just in case you’re wondering, I’m talking about Hammerhead in the Spider-Man/Marvel universe who looks like this:
Not the Aquaman villain King Shark who occasionally looks like a literal hammerhead shark with legs.
You want to fight that guy? Easy – just exploit his visual issues. Binocular, stereo vision is not his high point.
Back to Spider-Man’s Hammerhead – he’s been playing a role in the more recent issues of Spider-Man as the enforcer for the Black Cat. This, of course, has brought him into conflict with Spider-Man (Miles Morales) and his amazing friends on more than one occasion.
Before we start sciencing, let’s give it up for Hammerhead’s depiction in Spider-Man. Early on, Hammerhead was a buffoon, dressing, looking and talking like a 1930s gangster. He survived some weird storylines along the way (getting his brain transplanted into an adamantium skeleton by Mr. Negative), and for what seemed to be a one-note character who was ripped off of some Dick Tracy themes, Hammerhead has been established as one of Spider-Man’s solid foes. He’s had many storylines through the years, some of them, pretty great.
Hammerhead has really found his voice with writer Brian Bendis. He’s kept Hammerhead as amainstay in Spider-Man comic for over a decade, and his portrayal in the latest run of Spider-Man has continued the character’s solid representations. Thanks to Bendis and initial series artist Sara Pichelli, Hammerhead comes across with a distinctive voice. Read the comics – you’ll see what we’re talking about. He’s intimidating and menacing just as a guy, and then you remember, “Oh yeah, he’s got this battering ram for a head.”
Speaking of that head – it’s his main method of attack against super-powered folks. Any regular humans, he takes out with his fists – quite brutally. But for people like Spider-Man and his pals, they get the head.
Which is a hammer.
This all brings us to Spider-Man #17 (still in comic shops, or available here at Comixology). In it, Hammerhead goes after two heroes, Bombshell and Spider-Man (the Miles Morales one). And they both are much worse for the wear afterwards…well, if there is an afterwards.
Let’s look at the science of fighting Hammerhead.
Setting up some ground rules here:
- Hammerhead is, by Marvel.com’s description, an “Olympic level athlete,” which means we’re putting him at some fairly top running speeds, strengths and reaction times. Not to mention he’s got an adamantium (or adamantium-laced) skeleton which won’t break or compress under pressure. He’s tough.
-
Something is wonky with his weight as listed. He clocked in, according to Marvel.com’s wiki page on him, at 265 lbs (120 kg), but according to continuity, he’s a human brain inside an adamantium body. Adamantium is heavy stuff – case in point, Wolverine’s listed weight is at 300 lbs (136 kg), and Hammerhead has a good three to four inches on Wolverine. So – the mass of everything below is a little on the light side, but increasing Hammerhead’s mass only makes things worse for his victims. We’ll go with the 120 kg for the calculations, but they could be off.
- We’re working from a comic book, so we must make some estimations of flight times, reaction times and distances. As we move through the science, we’re going to point out how you can put in any number you want to check things out for yourself. Don’t buy my assumed times that Bombshell flew across the street, or that Hammerhead could/would hit Miles as fast as we estimated? No worries – put in your own numbers and see what you get. Trust me on this one though – all the end results are going to be bad for Hammerhead’s victims.
- I teach high school physics, so I’m going to approach this as a high school physics problem. Quite honestly, I’d have no problem handing this problem off to my students as a summative problem to review the concepts involved. YMMV, of course, but if you’re just reading this for fun – prepare to learn stuff!
Let’s get going.
Round 1: Hammerhead vs. Bombshell
Early on in the issue, Hammerhead goes up against Bombshell who tries to stop him with her…bomb…shells? Anyway, Hammerhead hits her twice, once into garbage and then the second time, across the street. She gets up from the first hit, but doesn’t from the second. Let’s look at the second hit.
To figure out some parts of the hit and the damage done to Bombshell, we can figure out a few things:
- Bombshell’s velocity across the street.
- The force with which Hammerhead hits Bombshell.
- The force Bombshell experienced when she came to a complete stop.
Why did the Bombshell cross the road?
Because Hammerhead hit her with his hammer…head.
This part is easy – Bombshell’s velocity across the street is her displacement divided by the time it took her to cross the street, or:
Velocity = displacement/time
The average street width in New York City is about 190 feet (about 58 meters).
Let’s say it took her 2 seconds to travel across the street (again, feel free to use your own numbers for her flight time if you think mine are off). So…
Velocity = 58 meters/2 seconds
Velocity = 29 m/s
That’s about 65 miles per hour.
Yikes.
How Hard Did He Hit Her?
To figure out the force with which Hammerhead hit Bombshell, we need to use the work-energy theorem. Simply, you have to do work on an object to give it energy. Bombshell is flying through the air at (we’re going to assume) a constant 29 m/s. She’s got a ton of kinetic energy. How much? Formula time:
Ek = ½(mass)(velocity)2
I’m ballparking Bombshell’s mass at 50 kg (which is about 110 pounds – she’s shown to be tall and thin), so:
Ek = ½(50kg)(29m/s)2
Ek = 21,025 Joules
This means that to get Bombshell’s mass moving that fast across the street, Hammerhead had to do 21,025 Joules of work on her. And from the work done, we can figure out the force he used to hit her. In its simple form:
Work = (Force)(distance)
(We’re assuming that Hammerhead’s hit was perfectly horizontal and in the same direction Bombshell moved, and yeah – in the issue, she’s shown moving toward him, but let’s keep things simple. If she was moving towards him when she got hit, that would bleed off some of her velocity, but the result would still be the same – she is going to fly across the street at a very unsafe speed.)
The value for distance here is not the 58 meters. The work Hammerhead did on Bombshell took place only while they were in direct contact, or rather, for the time of the “hit.” A hit is a push, and when Hammerhead “hit” Bombshell, he pushed her for a short distance before she flew away across the street.
Think of two people squaring up for a fight – one might push the other in the chest. Think of how long the hands are in constant with the chest, and try to estimate that distance. That’s the distance over which work was done.
How far did Hammerhead “push” Bombshell during the “hit?”
We’re going to be conservative and say 20 centimeters – a solid shove (again, if you’re not comfortable with that number, change it…but be warned – making that distance smaller only makes it worse for Bombshell).
Solving for force:
Force = work/distance
Force = 21,025 J/.20 m
Force = 105,125 N
That’s about 23,600 pounds, or about two smallish African Elephants slamming into you.
You’d fly across the street too.
Bonus – what was the acceleration Bombshell experienced when she was hit by that force?
That’s where we need Newton’s Second Law of Motion:
Force = (mass)(acceleration)
Solve for acceleration:
a = F/m
a = 105,125 N/50 kg
a = 2102.5 m/s2
Okay, okay, okay.
Yeah – that’s totally nuts. That’s like sprint missile-level acceleration. If a real human encountered that acceleration, they’d be a bag of pudding.
But please remember – Spider-Man #17 is a comic book and not a physics book. It’s not meant to be realistic. Special effects and things like this are metaphor or symbolic. They’re part of the language of comics – they’re meant to be exaggerated.
The Ride Comes to a Complete Stop
The force Bombshell encountered in that hit was only part of her problem. The other problem comes when she hits the light post on the far side of the street. She hits it with enough force to knock it over, something I’ve only really seen a car accomplish. So yeah…ouch.
So…that force?
This is a momentum-impulse issue right here. Every moving thing (like Bombshell) has momentum, which is the product of the object’s mass multiplied by its velocity. To change an object’s momentum, you need an impulse, which is a force applied over time. As a formula, it looks like this:
(Force)(time) = (mass)(change in velocity)
Change in velocity = 0 m/s – 29 m/s
To determine the force needed, we need to know the time. We’re going to estimate it took Bombshell about 0.1 seconds to come to a full stop when she hit the light post. Again – change the number if you’re not down with our estimate and see what happens.
So, that force:
F = (50 kg)(-29 m/s)/0.1 sec
F = -14,500 N (the negative sign means it’s in the opposite direction as her motion)
Roughly 3260 pounds of force.
Ouch.
But honestly, that was expected: 29 m/s is roughly 65 mph. Bombshell was essentially traveling 65 mph in a car that slammed into a wall.
On the plus side, her injuries are acknowledged in the issue:
Some final Bombshell thoughts:
Again, if you don’t dig my estimates, put your own in, and see what it does with the numbers. Don’t think she went across the street? Cool – decrease the distance (but keep it in meters). Don’t think Hammerhead “pushed” her that hard with the hit? Okay – put a smaller number in when calculating the force from the work done.
It’s not going to end well for Bombshell. The result is that her 50 kg moves through the air for a sizable distance. You need a sizable force to do that. Same with her stop.
One more time – this is hugely not realistic at all. It’s a comic book. So why do it? Easy – the exaggeration drives home the connections. It makes a dry physics problem interesting. Or…more interesting than it was.
Now let’s talk about what happened to Miles.
Round 2: Hammerhead vs. Spider-Man (a.k.a. – “I’ve got a crushing injury on you.”)
Once Miles realizes that Hammerhead was behind the attack on Bombshell, he goes kind of…nuts, and mows through a gang of henchmen to finally square off against Hammerhead. The fight’s going well for Miles until he, as Hammerhead so nicely points out, “lets up.” Hammerhead gets the drop on Spidey, and then…well…
Let’s dig in.
Hammerhead’s head is adamantium, so there’s no compression. And, given his neck muscles, we’re going with the idea that there’s no give in his shoulders when he makes a move like this one. Basically, if he’s hitting you like this, you’re getting all the force. To make things worse, all of that force is concentrated to an area that’s about the size of a dessert plate. To make things even worse, Miles is getting hit right on his chest, which is all kinds of bad news.
First things first, let’s simplify things. From the image, Hammerhead is coming in along a straight, horizontal path, so we’re going to assume all of his force is going towards Spider-Man. We’re not going to worry about any angles of attack here – it’s all going right in…to Miles. And given that he’s lined himself up horizontally, we’re going with the idea that Hammerhead’s acting, basically, like a piston, and that his entire mass is behind this hit (again, if that makes you feel funny – give it a try with your own numbers for mass and see what you get). It’s a bit of a fudge factor on my part, but I’m okay with it.
Setting things up, immediately before the hit, Hammerhead is at an arm’s length (my arm is about 80 cm long, so 0.8 m) from Miles, so that’s the distance he covers. Hammerhead hits Miles and comes to a complete stop, so that’s helpful.
For this to be effective, or at least as effective as it looks, it needs to be quick. Bruce Lee one-inch-punch quick. Like a snake quick.
To calculate this, we’re once again going to go with momentum and impulse. We need a couple of times – how long it took Hammerhead to move that distance of his arm, and then an estimate of how long he was impacting against Miles.
As for the time it takes Hammerhead to get his head to Miles, I’m going with something smaller than a second (which is the value I got when I tried it). First – there are speed lines in the panel – those indicate that he’s moving fast. Secondly, he’s an Olympic level athlete. He’s pushing with Olympic level athlete legs. Pushing with more force with his legs is going to make the travel time less, thus increasing his speed.
Your mileage may vary, but I’ll give him 0.07 seconds to move from an arm’s length to Miles’ chest. It’s pretty quick, but again…Olympic level athlete. So therefore,
velocity = 0.8 m/0.07 second
v = 11.42 m/s
So Hammerhead’s head is coming in at 11.42 m/s. That’s pretty quick.
Let’s use the momentum again to figure out the force Miles’ experiences.
We need a time for impact, and I’m going small because Hammerhead is a pro at this, so let’s make it the same 0.1 seconds as above. He hits quick and backs off.
Once again – force from momentum and impulse:
F = mΔv/t
F = (120 kg)(11.42 m/s)/0.1 s
F = 13704 N
That’s not…comfortable. Like over 3000 pounds of not comfortable.
But remember – that force would be for the entirety of Hammerhead hitting Spider-Man. Hammerhead only hits with the top of his head, which, judging from the panel, looks to have a diameter of about 22 cm (so a radius of 11 cm or .11 m). Now we’re talking about pressure.
Pressure = force/area
Area of the top of Hammerhead’s head (it’s a circle) = πr2
A = π(.11 m)2
A = 0.04 m2
So now – pressure…
P = 13704 N/0.04 m2
P = 342,600 Pascals
That’s about 50 pounds per square inch. Per square inch, remember – Miles still has all of that force pressing in on him, the pressure number just breaks it down into bits.
And of course, what makes it all worse is that Miles is pressed up against a stone (I think) column which looks to be pretty non-compressible and is actually cracking from the strain of Hammerhead’s hit (with Miles in the way). Your physics brain is engaged enough by this point to figure out what that means for the Miles sandwich.
What does all of this mean?
Well, if this was our world, Miles’ ribs are broken, easy. Ribs are pretty easy to break. Remember your CPR course? More than 125 pounds of pressure on the ribs is enough to break them. In fact, rib fractures are common co-injuries of a heart attack where CPR is performed.
In addition to rib fractures (which make it really hard to breathe), Miles probably had the wind knocked out of him by the impact. Strong impacts to the abdominal area can temporarily paralyze the diaphragm, making it impossible – for a moment or two – to catch your breath. Miles’ internal organs would be bruised, some – like his lungs – could be ruptured, and there’s a good chance that major blood vessels could have been torn by the impact.
If this is all starting to sound like something you hear in high school, it’s basically because it’s what happens when someone slams into the steering wheel of a car during an accident.
One of the other rare, but possible dangers of this hit is commotio cordis, which causes the heart to go into immediate cardiac arrest if the hit comes at the right time in the cardiac cycle (the specific order of atria and ventricles contracting, one after the other). This injury is seen most often in sports following a powerful hit to the chest from another player, or even a baseball (or a whipped cream container) . It has an 85% fatality rate.
So – where does this leave us?
Hammerhead is pretty darn dangerous. He’s a very strong guy walking around with an unbreakable blunt instrument that he’s an expert at using. He’s fast and he knows what to do with his strength and speed. End result – he’s deadly, and if the Marvel Universe shared our physics, Hammerhead would be responsible for the deaths of many heroes. Think about it – he looks like a rejected Dick Tracy villain. If you were looking to up your street cred like Bombshell was, Hammherhead looks to be an easy target.
Yeah, oops.
Real physics-wise, impact forces, momentum and energy all follow rules that are easy to apply and calculate with the right tools. As I’ve mentioned a few times now, if you want to see what would happen if Hammerhead increased his impact time, ran slower towards Bombshell, wasn’t as quick hitting Spider-Man or anything else, be my guest. You’re only going to get smarter, and you’ll see that fighting Hammerhead, unless you’re taking away his means of locomotion (hint, hint, Spidey…hips, knees and ankles…) is a losing proposition.
Teacher Talk: Why I Dig This Problem
As I mentioned above, I teach physics. Would I use this sequence in my class? You bet.
How?
Sometime after we’d talked about energy conservation, momentum and motion, I’d set the scene for Bombshell and Spider-Man and let my students go at it. I wouldn’t give them estimates. They’d have to figure them out, and that, for me, is one of the strengths of using problems like this in class. Students lock themselves into thinking about problems in “textbook form” with no estimation or reasoning necessary. So, I’d give them nothing in terms of impact times, speeds, or the length of Hammerhead’s arm. I’d treat it like a modified PBL exercise, and if they come to me asking for help once they realized something was missing, point them toward a resource.
Oh, they’ll struggle, but in the end, they’ll be better for it.
How Does He Read a Book?
His eyes are literally looking perpendicular to where the book is.