You’ve seen it before, in many different forms. The hero, the villain…someone…lifts their opponent up by the collar, by the neck, by one body part, or in this case, by the sword.
Like all iconic and cool shots, it’s a power pose – all about expressing something about the character, rather than depicting something that could literally happen. It’s a metaphor representing overwhelming power on the part of the lifter and weakness on the part of the liftee. When it appears in a scene, the image should speak to a part of you that gets it. Without words, you know that the character doing the lifting is formidable, and the character in the air poses no threat. At the very least, seeing the image should trip something in your brain that says, “that’s just not possible.”
And that part of your brain is correct.
So – all that said about the image being metaphorical rather than literal, does that mean we’re not going to look at the science and numbers behind it?
This page isn’t called “The Metaphor Of.” Heck yeah, we’re going to look at it.
Before we get rolling, some of the other more famous “power lifts” you may have seen would of course include: Darth Vader, Arnold Schwarzenegger, Luke Cage, Beast, and…well, take your pick. It’s such a common element in storytelling it has its own entry in TV Tropes – Neck Lift.
First off – don’t get us wrong here – the neck lift can be done in real life without any kind of tricks. To do it, the liftee must have a significantly smaller mass than the lifter. But that’s not what you see, right? Most often, it’s two of the same-sized characters, one whose feet are a-danglin’, and the other who’s sneering in that menacing way. To make it work with two individuals of roughly the same size, one must have a mass that’s larger (often significantly) than the other. Strength’s important, but it’s not the main thing here.
And hey – just between us pals here, never, ever do this to another person. Just…don’t. There are way too many things that can go wrong, and our bodies are not made to be hung by the neck – it’s why hanging is a pretty effective means of execution, after all. “Yeah, but I saw it on…” What you saw was two professionals who performed a trick to make you think that you saw what you thought you saw. Just don’t, okay?
We’ll get to the math and physics in a minute. What’s going on with our example here?
The image comes from DC’s The Wildstorm #9. The guy with the sword is one John Colt, a Kherubim alien from the planet Khera. In the issue, Colt is reminiscing about a battle he had while recovering a Kherubim artifact from its guards in medieval Japan. Following some serious swordplay, Colt squared off against his final two opponents, skewering one, and then running his sword through the second. He showed off by lifting the two dead men with one arm, and then swung his arm, letting them slide off his sword in the process.
So – let’s use this as the example of the one-handed lift. And just to be clear – whether you’re lifting with a hand to the neck, by grabbing the collar, holding a leg, or like we’re seeing here – two guys impaled on a sword…the concept and approach is all the same. What we’re deal with is torque.
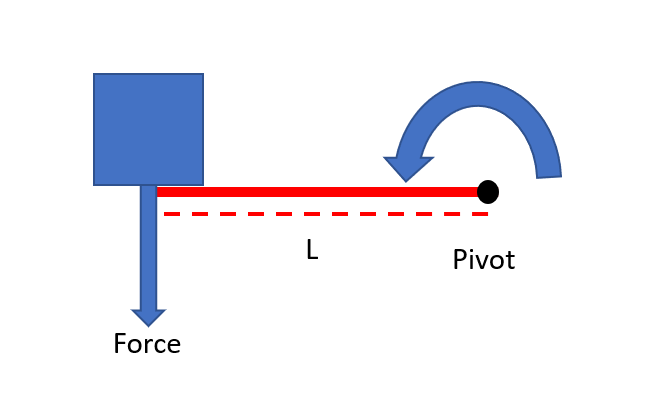
For a simple definition of torque, think of it as a force causing a rotation around a center of mass. To put a number to it, think of the formula as this:
Torque = force x lever arm
Where the lever arm equals the distance between where the force is applied and the points around which it would rotate, also known as the axis of rotation. To make things work, the force being applied and the lever arm are perpendicular to one another. A simple example is:
Multiply the force by the length of the lever arm, and you have a value for torque. If the pivot point is attached, the object will spin around it. For example, if the image represented a box sitting on an arm that was attached to a wall, the force in the illustration would be the box’s weight which is applied perpendicular to the arm. Simple, right?
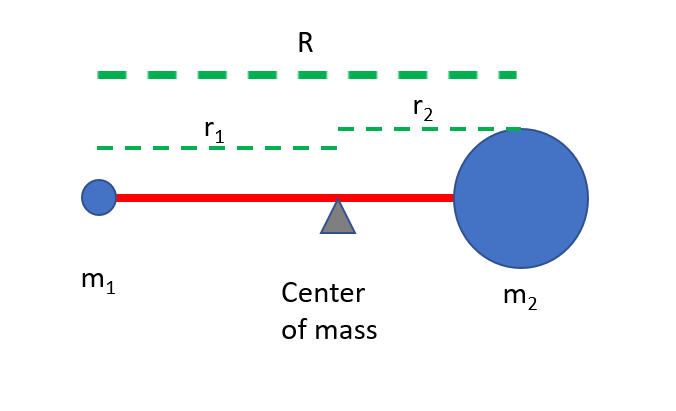
Let’s say that, instead of talking about one object, we’re talking about two that are connected. Now we’ve got a system. If force(s) are applied to either object, the objects will rotate around the center of mass of the system. Think of the center of mass as the pivot point of a seesaw, or, between two bodies, the mean location of their individual centers of mass. Like so:
In the illustration above, the center of mass is a closer to m2, the larger mass, because m2 contributes more to the total mass of the system, and thus has a stronger effect on the average. A force applied to either m1 or m2 will cause the system to rotate around the center of mass, which acts as the pivot point. The respective torque can be calculated by multiplying the force on m1 by R1 and the force on m2 by R2.
If we want to calculate the mass of one of the objects, and we know the mass of the other along with the respective distances between the objects and the center of mass, then we can use the formula:
m1r1 = m2r2
For a system with two masses, as shown above, to be balanced, the respective torques must be equal. The spin clockwise must equal the spin counterclockwise, and because of the two torques being equal, but in the opposite directions, there will be no rotation around the center of mass – or uniform rotation around the center of mass, but let’s leave that for another day. For today – holding up bad guys by the throat…or arm…we want there to be no rotation.
How do we apply what we now know about torque and center of mass to the power pose we’ve been talking about?
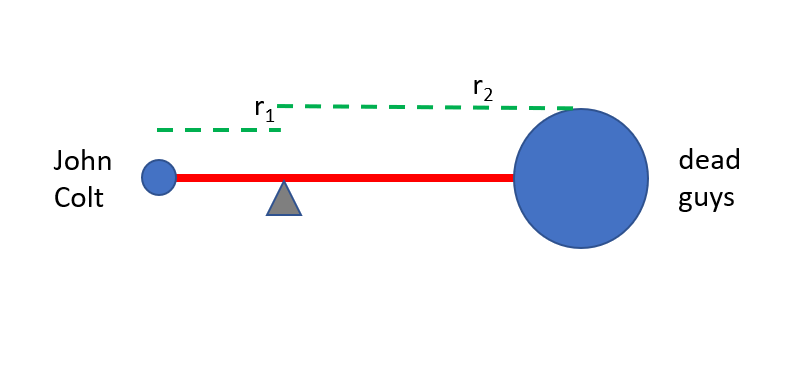
Remember this picture?
John Colt is m1 and the two dead guys on his sword are combined as m2. The system isn’t floating freely in space, the point around which the system wants to rotate is the forwardmost toe of John’s left foot. If John’s going to tip over to his left, he’s going to pivot around that point. We’re going to assume that the centers of mass are in a straight line with one another. Not a 100% accurate assumption, but we can live with it. Or, basically:
And translating that to our image:
A weird thing happened here – the center of mass shifted from being closer to the dead guys (the larger mass) to being closer to John (what we would think was the smaller mass). That will all become apparent in a minute or two.
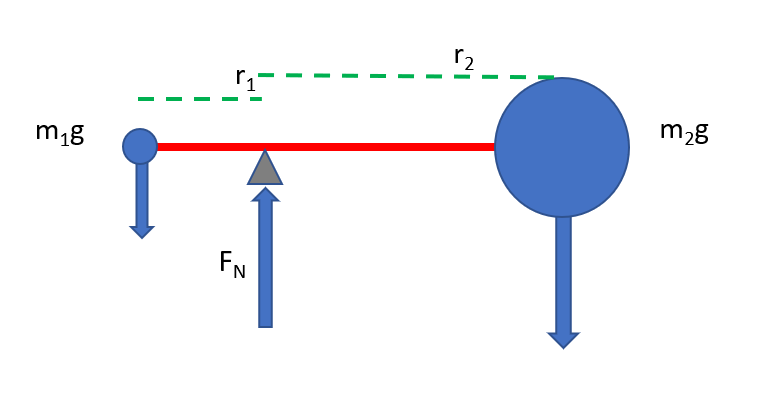
There are three forces acting on this system – gravitational forces on John and on the dead bad guys, and the force of the ground pushing up on the point of rotation (called the normal force). The center of mass is located somewhere between John and the dead bad guys, on an imaginary line that connects them, and it’s directly above the point of rotation (John’s toes). The important thing here is that our John-bad guys system is in equilibrium, meaning that there’s no rotation around the center of mass. The torque from the forces acting to spin the system (the gravitational forces) must add up to zero.
While it’s not 100% accurate, think of it this way – if the John-bad guy system was in space (gross, but go with it), and you pushed on one or the other, the system would spin around the center of mass. In space. Forever, until acted upon by an outside force.
If we’re looking at forces:
Going back to the formula:
m1r1 = m2r2
m1 = John
m2 = Bad guys
r1 = distance from John’s center of mass to the center of mass of the system
r2 = distance from the center of mass of the bad guys to the center of mass of the system.
Typically, when standing with arms up, a human’s center of mass is just above the navel. We can reduce John to a sphere for simplicity, and keep our line straight from his center of mass to the system’s center of mass, and come up with about .36 m.
As for our bad guys, the center of mass of them would be somewhere between the two of them, pretty much in line with John’s arm, so let’s go with an approximate value of .93 m.
Mass of the (combined) bad guys – they don’t look particularly buff, but they’re tough fighters, so let’s go with 75 kg each for an m2 total of 150 kg.
As always, if you’re not cool with the numbers we’re putting in, go with you own, recalculate and see what you get.
About those distances? Using a model with a sword (okay, it was me, and it was a Nerf sword), so the numbers are fairly accurate.
Solving our earlier equation for m1 (John’s mass):
m1 = m2r2/r1
m1 = (150)(.93)/.36
m1 = 388 kg
Or, roughly, 855 lbs.
That’s a lot. And that’s just the lower limit. He could be more than 855 lbs, easily. But if he was less, he would tip over on his pivot point, his toes.
If you want, you can adjust the r values and see what that does to John’s mass, but if you increase his weight, the center of mass will shift closer to him and make the r1 value smaller. If John was lighter, the value of r1 would have to increase, or visually, his legs would have to be spread farther apart (to make r1 longer).
But remember, in the visual language of comics (or movies, or TV, or wherever you find this pose), this image is as much (or more) a metaphor as it is meant to be a literal interpretation.
And – the calculation we’ve just done here isn’t specific to John Colt and the dead bad guys. It works for everyone/everything that is in a position such as this. At WIRED, Rhett Allain has looked at Darth Vader, Luke Cage and Arnold Schwarzenegger in variations of this pose, and as mentioned above, the pose occurs so often in pop culture, it has its own page at TV Tropes and goes by different names in different forms of media.
So keep an eye out, and you’ll spot the neck grab and all its variations everywhere in pop culture.
Honestly – we didn’t even have to wait too long for another appearance – in episode 9 of the current season (3) of Supergirl, the villain Reign holds Kara off the edge of a building after thoroughly defeating her. Eyeball some distances, estimate (or look up Supergirl’s mass), and you can calculate Reign’s mass. We’d bet she’s not a lithe little thing.